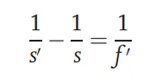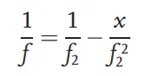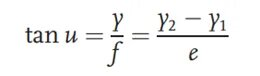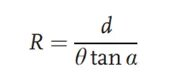Optiliste süsteemide fookuskauguse määratlus ja testimismeetodid

1. Optiliste süsteemide fookuskaugus

Fookuskaugus on optilise süsteemi väga oluline näitaja, fookuskauguse kontseptsioonist on meil enam-vähem arusaam, mida me siinkohal vaatame üle.
Optilise süsteemi fookuskaugus, mis on defineeritud kui kaugus optilise süsteemi optilisest keskpunktist kiire fookuseni paralleelse valguse langemisel, on valguse kontsentratsiooni või hajumise mõõt optilises süsteemis. Selle kontseptsiooni illustreerimiseks kasutame järgmist diagrammi.

Ülaltoodud joonisel koondub vasakult otsast langev paralleelkiir pärast optilise süsteemi läbimist kujutise fookuspunkti F', koonduva kiire vastassuunaline pikendusjoon lõikub langeva paralleelkiire vastava pikendusjoonega ühes punktis ning pinda, mis läbib seda punkti ja on risti optilise teljega, nimetatakse tagumiseks peatasandiks, tagumine peatasandik lõikub optilise teljega punktis P2, mida nimetatakse põhipunktiks (või optiliseks keskpunktiks), põhipunkti ja kujutise fookuse vaheline kaugus on see, mida me tavaliselt nimetame fookuskauguseks, täisnimi on kujutise efektiivne fookuskaugus.
Jooniselt on samuti näha, et kaugust optilise süsteemi viimasest pinnast kujutise fookuspunktini F' nimetatakse tagumiseks fookuskauguseks (BFL). Vastavalt sellele, kui paralleelne kiir langeb paremalt poolt, on olemas ka efektiivse fookuskauguse ja eesmise fookuskauguse (FFL) mõisted.

2. Fookuskauguse testimise meetodid

Praktikas on optiliste süsteemide fookuskauguse testimiseks palju meetodeid. Erinevate põhimõtete alusel saab fookuskauguse testimise meetodid jagada kolme kategooriasse. Esimene kategooria põhineb pilditasandi asukohal, teine ​​kategooria kasutab fookuskauguse väärtuse saamiseks suurenduse ja fookuskauguse vahelist seost ning kolmas kategooria kasutab fookuskauguse väärtuse saamiseks koonduva valgusvihu lainefrondi kõverust.
Selles osas tutvustame optiliste süsteemide fookuskauguse testimiseks tavaliselt kasutatavaid meetodeid:

2.1Collimeeri meetod

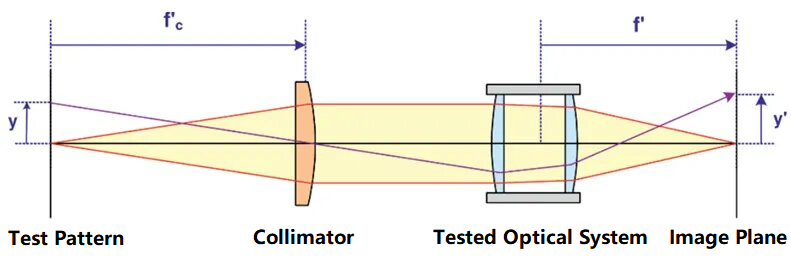
Kollimaatori kasutamise põhimõte optilise süsteemi fookuskauguse testimiseks on näidatud alloleval diagrammil:

Joonisel on testmuster paigutatud kollimaatori fookusesse. Testmustri kõrgus y ja fookuskaugus f_cKollimaatori fookuskaugused on teada. Pärast seda, kui kollimaatori kiiratud paralleelne kiir on testitud optilise süsteemi poolt koondatud ja pilditasandil kujutatud, saab optilise süsteemi fookuskauguse arvutada pilditasandil oleva testmustri kõrguse y' põhjal. Testitud optilise süsteemi fookuskauguse saab arvutada järgmise valemi abil:

2.2 GaussiMmeetod
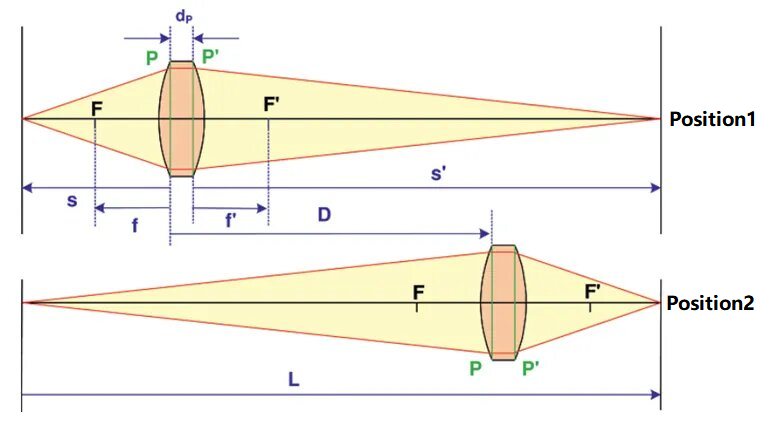
Gaussi meetodi skemaatiline joonis optilise süsteemi fookuskauguse testimiseks on näidatud allpool:

Joonisel on testitava optilise süsteemi eesmine ja tagumine peatesapind tähistatud vastavalt tähtedega P ja P' ning kahe peatesapinna vaheline kaugus on d._PSelle meetodi puhul d väärtus_Ploetakse teadaolevaks või on selle väärtus väike ja seda võib ignoreerida. Vasakule ja paremale otsale asetatakse objekt ja vastuvõtuekraan ning nende vaheline kaugus registreeritakse kui L, kus L peab olema suurem kui testitava süsteemi neljakordne fookuskaugus. Testitavat süsteemi saab paigutada kahte asendisse, mida tähistatakse vastavalt positsiooniga 1 ja positsiooniga 2. Vasakpoolset objekti saab vastuvõtuekraanil selgelt kujutada. Nende kahe asukoha vahelist kaugust (tähistatud kui D) saab mõõta. Konjugeeritud seose kohaselt saame:

Nendes kahes positsioonis registreeritakse objektide kaugused vastavalt s1 ja s2, seejärel s2 - s1 = D. Valemi tuletamise abil saame optilise süsteemi fookuskauguse järgmiselt:

2.3Lensomeeter
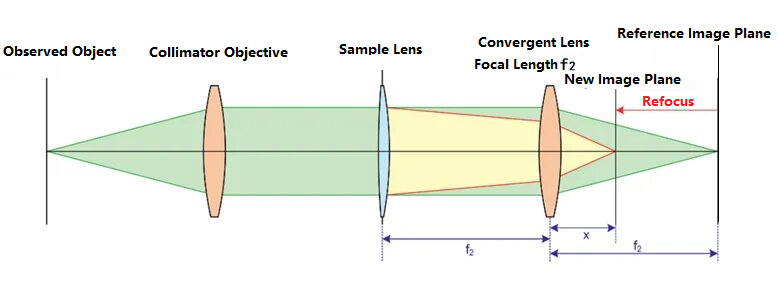
Läätsemeeter sobib väga hästi pika fookuskaugusega optiliste süsteemide testimiseks. Selle skemaatiline joonis on järgmine:

Esiteks ei asetata testitavat läätse optilisele teele. Vasakul asuv vaadeldav sihtmärk läbib kollimeeriva läätse ja muutub paralleelseks valguseks. Paralleelset valgust koondab koondav lääts, mille fookuskaugus on f.₂ja moodustab võrdluspildi tasapinnal selge pildi. Pärast optilise tee kalibreerimist asetatakse testitav lääts optilisele teele ning testitava läätse ja koondava läätse vaheline kaugus on f₂Selle tulemusel fokusseeritakse testitava läätse toimel valguskiir ümber, põhjustades kujutistasandi asendi nihke, mille tulemuseks on diagrammil uue kujutistasandi asukohas selge kujutis. Uue kujutistasandi ja koondava läätse vahelist kaugust tähistatakse tähega x. Objekti ja kujutise suhte põhjal saab testitava läätse fookuskauguse tuletada järgmiselt:

Praktikas on läätsemõõturit laialdaselt kasutatud prilliläätsede fookuskauguse mõõtmiseks ning selle eelised on lihtne kasutamine ja usaldusväärne täpsus.

2.4 AbbeRefraktomeeter

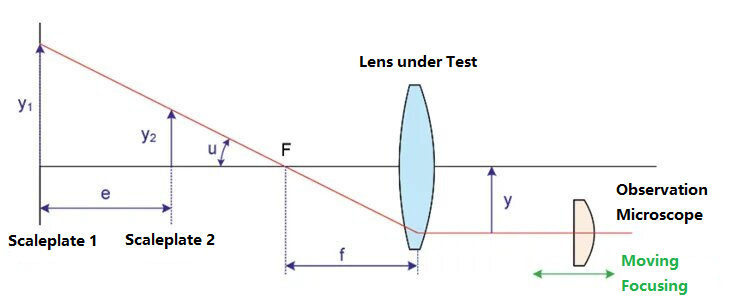
Abbe'i refraktomeeter on veel üks meetod optiliste süsteemide fookuskauguse testimiseks. Selle skemaatiline joonis on järgmine:

Asetage testitava läätse objektipinna poolele kaks erineva kõrgusega joonlauda, ​​nimelt skaalaplaat 1 ja skaalaplaat 2. Vastavad skaalaplaatide kõrgused on y1 ja y2. Kahe skaalaplaadi vaheline kaugus on e ja joonlaua ülemise joone ja optilise telje vaheline nurk on u. Skaalaplaati kujutab testitav lääts fookuskaugusega f. Kujutise pinna otsa on paigaldatud mikroskoop. Mikroskoobi asendit muutes leitakse kahe skaalaplaadi ülemised kujutised. Sel ajal tähistatakse mikroskoobi ja optilise telje vahelist kaugust y-ga. Objekti ja kujutise suhte põhjal saame fookuskauguse järgmiselt:

2.5 Moire'i deflektomeetriaMeetod
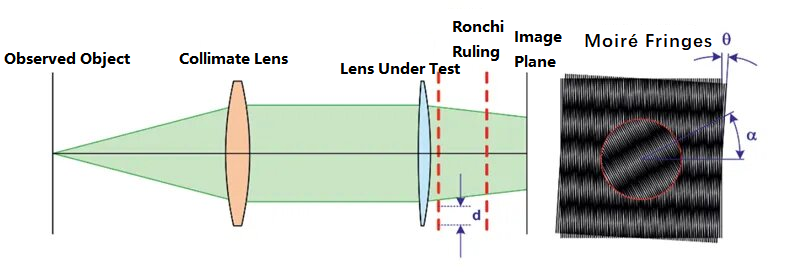
Moiré deflektomeetria meetod kasutab paralleelsetes valguskiirtes kahte Ronchi joonte komplekti. Ronchi joon on klaasist aluspinnale sadestatud kroommetallikile ruudukujuline muster, mida tavaliselt kasutatakse optiliste süsteemide toimivuse testimiseks. Meetod kasutab kahe võre poolt moodustatud Moiré triipude muutust optilise süsteemi fookuskauguse testimiseks. Põhimõtte skemaatiline diagramm on järgmine:

Ülaltoodud joonisel muutub vaadeldav objekt pärast kollimaatori läbimist paralleelseks kiireks. Optilisel teel, ilma testitavat läätse eelnevalt lisamata, läbib paralleelne kiir kahte võret nihkenurgaga θ ja võrede vahekaugusega d, moodustades pilditasandile Muaré triipude komplekti. Seejärel asetatakse testitav lääts optilisele teele. Algne kollimeeritud valgus annab pärast läätses murdumist teatud fookuskauguse. Valgusvihu kõverusraadiuse saab arvutada järgmise valemi abil:

Tavaliselt asetatakse testitav lääts esimesele võrele väga lähedale, seega vastab ülaltoodud valemis olev R väärtus läätse fookuskaugusele. Selle meetodi eeliseks on see, et sellega saab testida nii positiivse kui ka negatiivse fookuskaugusega süsteemide fookuskaugust.

2.6 OptilineFiberAutokollimatsioonMmeetod
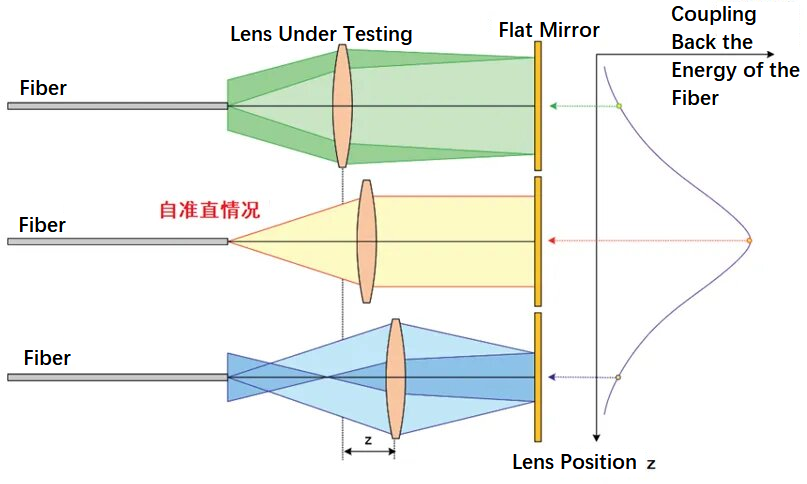
Alloleval joonisel on näidatud läätse fookuskauguse testimise põhimõte optilise kiu autokollimatsiooni meetodi abil. See kasutab fiiberoptikat, et kiirata hajuv kiir, mis läbib testitavat läätse ja seejärel suunatakse tasapinnalisele peeglile. Joonisel olevad kolm optilist rada esindavad vastavalt optilise kiu tingimusi fookuses, fookuses ja fookusest väljaspool. Testitava läätse asendit edasi-tagasi liigutades saate leida kiupea asukoha fookuses. Sel ajal on kiir isekollimeeritud ja pärast tasapinnalise peegli peegeldumist naaseb suurem osa energiast kiupea asendisse. Meetod on põhimõtteliselt lihtne ja hõlpsasti rakendatav.

3. Kokkuvõte

Fookuskaugus on optilise süsteemi oluline parameeter. Selles artiklis kirjeldame üksikasjalikult optilise süsteemi fookuskauguse kontseptsiooni ja selle testimismeetodeid. Koos skemaatilise diagrammiga selgitame fookuskauguse määratlust, sealhulgas kujutisepoolse fookuskauguse, objektipoolse fookuskauguse ja eest-taha fookuskauguse mõisteid. Praktikas on optilise süsteemi fookuskauguse testimiseks palju meetodeid. See artikkel tutvustab kollimaatorimeetodi, Gaussi meetodi, fookuskauguse mõõtmise meetodi, Abbe'i fookuskauguse mõõtmise meetodi, Moiré läbipaindemeetodi ja optilise kiu autokollimatsioonimeetodi testimispõhimõtteid. Usun, et selle artikli lugemisega saate paremini aru optiliste süsteemide fookuskauguse parameetritest.